

# those formula at specific numeric value of p.
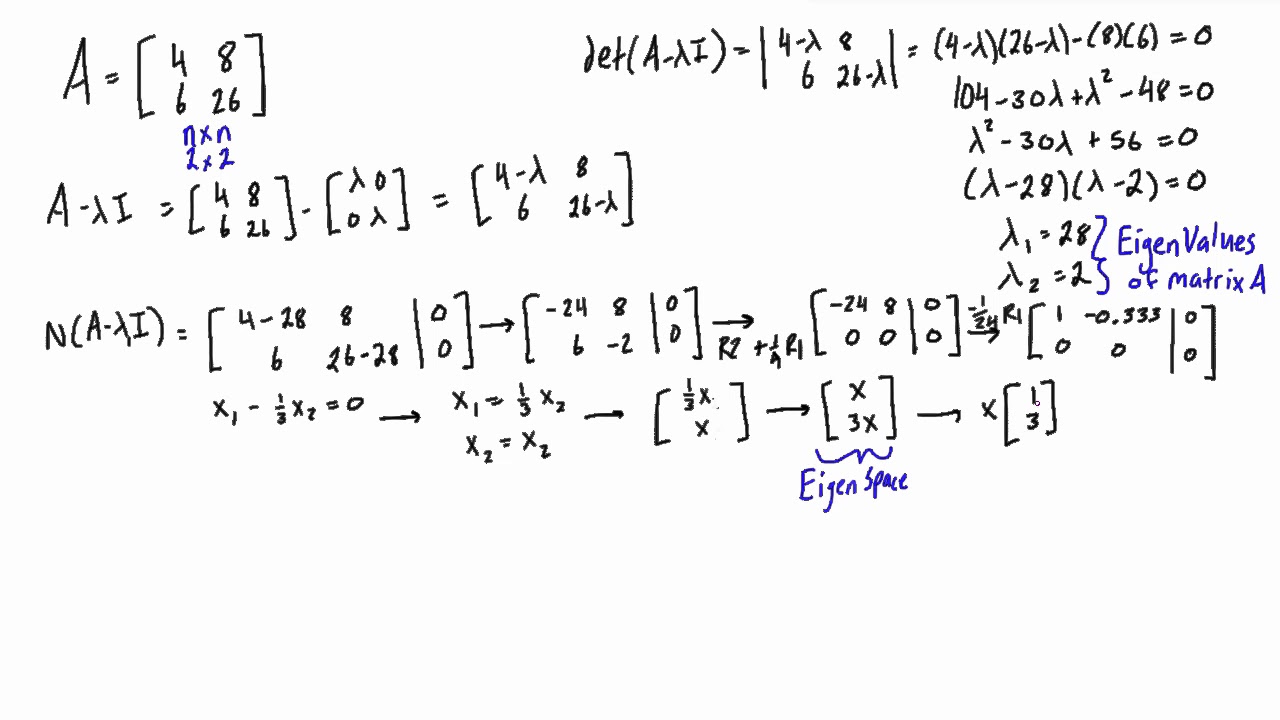
# small imaginary artefacts produced when evaluating # Extra precision is taken, to try and deal with # for the eigenvalues, in terms of parameter p # This produces R, as explicit symbolic formulas restart Ĭp := collect(cp/lambda^2,lambda,factor): Here is revised code, with the now symmetric Matrix k. These need not produce nonzero imaginary component artefacts as noise due to roundoff error. It thus still may be superior to use a dedicated root-finder on the characteristic polynomial, or compute the eigenvalues numerically, following substitution at floating-point values of parameter p.

Note however that these involve radicals and the imaginary unit, and immediate substitution of a floating-point value for parameter p results in small nonzero imaginary component in the results (as numeric roundoff artefact). This results in 8 explicit formulas (in terms of parameter p) for the eigenvalues. That also allows the characteristic polynomial of the exact rational form of k+kG to factor symbolically w.r.t. Following clarification by the Original Poster I make an adjustment below to replace the former definition of the entry of Matrix k by the value for its entry. Is that intentional, or a mistake? (If k is intended to be symmetric then please clarify, because it means that k+kG can be cast as a Maple Matrix with shape=symmetric and the floating-point eigenvalue computation will be a little faster, produce no 0.0*I imaginary artefacts, and return sorted by default.) I could mention that kG is symmetric, and k is almost symmetric. KG := p/840*Matrix(,Ĭp := CharacteristicPolynomial(Q, lambda):Ĭp := lambda^2*collect(cp/lambda^2,lambda,factor)
#GET EIGENVALUES MATLAB CODE#
Perhaps the following code will help get you started. The corresponding values of v that satisfy the equation are the right eigenvectors. The values of that satisfy the equation are the eigenvalues. So you will need to substitute numeric values for p, in order to obtain the remaining eigenvalues as floating-point. The eigenvalue problem is to determine the solution to the equation Av v, where A is an n-by-n matrix, v is a column vector of length n, and is a scalar. If you convert all your floating-point coefficients to exact rationals then it appears that k+kG has eigenvalue zero with multiplicity of two.īut the characteristic polynomial that remains (after dividing out lambda^2) is of degree 6, and that does not appear to factor directly. I heard maple can solve this problem but I am amateur on maple. Or we can do it in python, using numpy’s () method.I have a problem to calculate eigenvalues of a symbolic matrix. The algorithms related to solving a linear system of equations are also described there. To find the eigenvectors is a matter of solving two linear systems of equations of the form \(A * x = b\):įrom a code perspective, if you want to do it in C, you take a look at my “academical” called nml. We define two matrices \(A\) and \(B\) as being similar if there exists a non-singular matrix \(X\) such that: \(B=X^=1\). A matrix \(A\) can be decomposed like: \(A = Q * R\), where \(R\) is an upper triangular matrix, and Q is an orthonormal matrix.īecause \(Q\) is orthonormal, it has a few unique properties:įrom a computational perspective, this leads to some advantages because the inverse of an orthonormal matrix is the same as its transpose. In case you haven’t done so, I recommend you to read the linked sub-chapters first, as it will be easier to follow through.Įven if it’s not very obvious, the QR Decomposition (\(A = Q * R\)) of a matrix \(A\) is useful to compute the eigenvalues/eigenvectors associated with \(A\).īut, let’s recap. In my last two articles, I’ve tried to explore some fundamental topics in linear algebra: QR Decomposition, linear transformations and Eigenvalues/Eigenvectors. Computing Eigenvalues and Eigenvectors using QR Decomposition matlab matrix linear-algebra eigenvector eigenvalue Share Improve this question Follow edited at 18:42 Amro 124k 25 242 453 asked at 13:46 kamaci 72.5k 69 227 365 Why dont you use sort () to make c purposely descending and ascending.


 0 kommentar(er)
0 kommentar(er)
